unknown

Essense of the method: The given problem is transformed into a new one by changing the region of solutions $tema5_EN_files\tema5_EN_MathML_0.jpg$ into $tema5_EN_files\tema5_EN_MathML_1.jpg$ so that every element $tema5_EN_files\tema5_EN_MathML_2.jpg$ corresponds to an element $tema5_EN_files\tema5_EN_MathML_3.jpg$ and follows a certain rule $tema5_EN_files\tema5_EN_MathML_4.jpg$ . Hence the set of solutions to the problem $tema5_EN_files\tema5_EN_MathML_5.jpg$ is transformed into a set of solutions $tema5_EN_files\tema5_EN_MathML_6.jpg$ by means of $tema5_EN_files\tema5_EN_MathML_7.jpg$ the sought set $tema5_EN_files\tema5_EN_MathML_8.jpg$ for the given problem is found. This correspondence between $tema5_EN_files\tema5_EN_MathML_9.jpg$ , defined by means of $tema5_EN_files\tema5_EN_MathML_10.jpg$ , is called susbstitution.

1 Solving equations or inequalities by means of introducing a new unknown quantity which are then reduced again to equations or inequalities

Solution The equation can be represented in the following way $tema5_EN_files\tema5_EN_MathML_12.jpg$ ( we use the identity $tema5_EN_files\tema5_EN_MathML_13.jpg$ ). What remains is for the reader to notice that $tema5_EN_files\tema5_EN_MathML_14.jpg$ . Then the given equation assumes a more agreeable form $tema5_EN_files\tema5_EN_MathML_15.jpg$

Obviously we make the substitution $tema5_EN_files\tema5_EN_MathML_16.jpg$ and after that we solve the equation $tema5_EN_files\tema5_EN_MathML_17.jpg$ . Its roots are $tema5_EN_files\tema5_EN_MathML_18.jpg$ and $tema5_EN_files\tema5_EN_MathML_19.jpg$ . What remains is to solve the quadratic equations $tema5_EN_files\tema5_EN_MathML_20.jpg$ and $tema5_EN_files\tema5_EN_MathML_21.jpg$ and to unite their solutions.

Solution

(variant 1) The arithmetic mean of 4,5,6 and 7 is 5.5. We make the substitution $tema5_EN_files\tema5_EN_MathML_23.jpg$ and reduce the equation to the nicer $tema5_EN_files\tema5_EN_MathML_24.jpg$ , the solution to which is easy to find.

(variant 2) Multiplying $tema5_EN_files\tema5_EN_MathML_25.jpg$ and $tema5_EN_files\tema5_EN_MathML_26.jpg$ the given equation is transformed into $tema5_EN_files\tema5_EN_MathML_27.jpg$ We have to good possibilities for substitution $tema5_EN_files\tema5_EN_MathML_28.jpg$ or $tema5_EN_files\tema5_EN_MathML_29.jpg$

Solution
If you notice that you can represent the equation in the form $tema5_EN_files\tema5_EN_MathML_31.jpg$ then the substitution $tema5_EN_files\tema5_EN_MathML_32.jpg$ will be useful $tema5_EN_files\tema5_EN_MathML_33.jpg$ $tema5_EN_files\tema5_EN_MathML_34.jpg$

Solution
With a bit more resourcefulness the given inequality will look like this $tema5_EN_files\tema5_EN_MathML_36.jpg$ or $tema5_EN_files\tema5_EN_MathML_37.jpg$

A suitable subsititution is $tema5_EN_files\tema5_EN_MathML_38.jpg$ . Now we will solve the quadratic inequality $tema5_EN_files\tema5_EN_MathML_39.jpg$

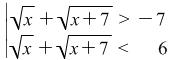Going back to the unknown quantity $tema5_EN_files\tema5_EN_MathML_40.jpg$ $tema5_EN_files\tema5_EN_MathML_41.jpg$ it is necessary to solve a double inequality $tema5_EN_files\tema5_EN_MathML_42.jpg$ which is the same as the following system $tema5_EN_files\tema5_EN_MathML_43.jpg$ .

After finding the solutions to each of the inequalities and then take their intersection you get the answer $tema5_EN_files\tema5_EN_MathML_44.jpg$ .

Example 1.5.

Solve the equation $tema5_EN_files\tema5_EN_MathML_45.jpg$

Hint If we add to both sides of the expression $tema5_EN_files\tema5_EN_MathML_46.jpg$ (doubled product) we get $tema5_EN_files\tema5_EN_MathML_47.jpg$ or $tema5_EN_files\tema5_EN_MathML_48.jpg$

If you notice that $tema5_EN_files\tema5_EN_MathML_49.jpg$ $tema5_EN_files\tema5_EN_MathML_50.jpg$ , then the previous equation will look like this $tema5_EN_files\tema5_EN_MathML_51.jpg$ Of course the substitution is $tema5_EN_files\tema5_EN_MathML_52.jpg$

Example 1.6.

Solve the equation $tema5_EN_files\tema5_EN_MathML_53.jpg$

Hint We replace the equation with its equivalent $tema5_EN_files\tema5_EN_MathML_54.jpg$ The substitution is $tema5_EN_files\tema5_EN_MathML_55.jpg$ .

Problems for individual work

2 Solving equations by means of substitutions which are reduced to solving systems

Solution
(variant 1) A suitable substitution is $tema5_EN_files\tema5_EN_MathML_61.jpg$

We get the following system of equations 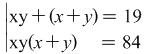$tema5_EN_files\tema5_EN_MathML_62.jpg$ . Let $tema5_EN_files\tema5_EN_MathML_63.jpg$ and $tema5_EN_files\tema5_EN_MathML_64.jpg$ .

The system now looks like this 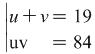$tema5_EN_files\tema5_EN_MathML_65.jpg$ . This way it is pleasing to be looked at as well as to be solved.

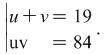
(variant 2) We make the substitutions directly $tema5_EN_files\tema5_EN_MathML_66.jpg$ и $tema5_EN_files\tema5_EN_MathML_67.jpg$ and get the system $tema5_EN_files\tema5_EN_MathML_68.jpg$

After solving it the solutions to the given equation are found through the equations $tema5_EN_files\tema5_EN_MathML_69.jpg$ and $tema5_EN_files\tema5_EN_MathML_70.jpg$

Solution Let $tema5_EN_files\tema5_EN_MathML_73.jpg$ and $tema5_EN_files\tema5_EN_MathML_74.jpg$ . Then the equation will look like this $tema5_EN_files\tema5_EN_MathML_75.jpg$ The second equation for $tema5_EN_files\tema5_EN_MathML_76.jpg$ and $tema5_EN_files\tema5_EN_MathML_77.jpg$ we will get when we multiply $tema5_EN_files\tema5_EN_MathML_78.jpg$ and $tema5_EN_files\tema5_EN_MathML_79.jpg$ respectively with $tema5_EN_files\tema5_EN_MathML_80.jpg$ and $tema5_EN_files\tema5_EN_MathML_81.jpg$ and then add them together. The result is $tema5_EN_files\tema5_EN_MathML_82.jpg$ , i.e. 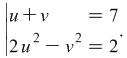the system is $tema5_EN_files\tema5_EN_MathML_83.jpg$ After determining $tema5_EN_files\tema5_EN_MathML_84.jpg$ and $tema5_EN_files\tema5_EN_MathML_85.jpg$ and going back to the substitutions it is easy to find that $tema5_EN_files\tema5_EN_MathML_86.jpg$ .

Solution Let $tema5_EN_files\tema5_EN_MathML_88.jpg$ and $tema5_EN_files\tema5_EN_MathML_89.jpg$ Then the given equation will look like this $tema5_EN_files\tema5_EN_MathML_90.jpg$ . The second equation for $tema5_EN_files\tema5_EN_MathML_91.jpg$ and $tema5_EN_files\tema5_EN_MathML_92.jpg$ we will get by adding together term by term $tema5_EN_files\tema5_EN_MathML_93.jpg$ and $tema5_EN_files\tema5_EN_MathML_94.jpg$ , i.e. $tema5_EN_files\tema5_EN_MathML_95.jpg$ . 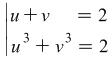The result is the following system $tema5_EN_files\tema5_EN_MathML_96.jpg$ whose solutions are $tema5_EN_files\tema5_EN_MathML_97.jpg$ . Going back to the substitutions we find that $tema5_EN_files\tema5_EN_MathML_98.jpg$ .

Example 2.4.

Solve the equation $tema5_EN_files\tema5_EN_MathML_99.jpg$ .

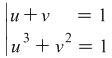Hint We make the substitutions $tema5_EN_files\tema5_EN_MathML_100.jpg$ and $tema5_EN_files\tema5_EN_MathML_101.jpg$ and solve the following system $tema5_EN_files\tema5_EN_MathML_102.jpg$ .

Answer $tema5_EN_files\tema5_EN_MathML_103.jpg$ .

Problems for individual work

3 Solving some systems of equations by means of partial substitution (in one of the equations of the system) or global substitution (in each of the equations of the system)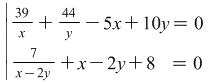

Solution The system can be written down in the form 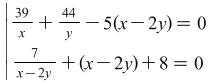$tema5_EN_files\tema5_EN_MathML_108.jpg$ .

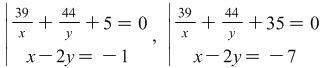A suitable substitution is $tema5_EN_files\tema5_EN_MathML_109.jpg$ . Then the second equation of the system will look like this $tema5_EN_files\tema5_EN_MathML_110.jpg$ . Later on the set of solutions of the system becomes a union of the sets of solutions of the systems $tema5_EN_files\tema5_EN_MathML_111.jpg$ :

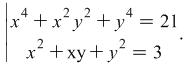
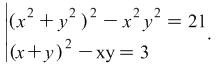Solution Notice that the left sides of both equations are symmetric expressions in regard to $tema5_EN_files\tema5_EN_MathML_113.jpg$ and $tema5_EN_files\tema5_EN_MathML_114.jpg$ . To solve such systems substitutions $tema5_EN_files\tema5_EN_MathML_115.jpg$ and $tema5_EN_files\tema5_EN_MathML_116.jpg$ are used. Before that we will replace the system with its equivalent system $tema5_EN_files\tema5_EN_MathML_117.jpg$ (We bring to notice that $tema5_EN_files\tema5_EN_MathML_118.jpg$ and $tema5_EN_files\tema5_EN_MathML_119.jpg$ ).

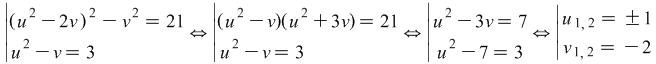
We make the substitutions $tema5_EN_files\tema5_EN_MathML_120.jpg$ and $tema5_EN_files\tema5_EN_MathML_121.jpg$ and solve the system $tema5_EN_files\tema5_EN_MathML_122.jpg$

In the end we have to solve the systems 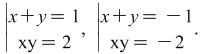$tema5_EN_files\tema5_EN_MathML_123.jpg$ Notice that if $tema5_EN_files\tema5_EN_MathML_124.jpg$ and $tema5_EN_files\tema5_EN_MathML_125.jpg$ are the respective sets of solutions to the last two systems, then the solution of the given system is the set $tema5_EN_files\tema5_EN_MathML_126.jpg$ .

Problems for individual work

Exercise 3.1. Solve the system 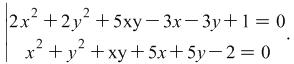$tema5_EN_files\tema5_EN_MathML_127.jpg$

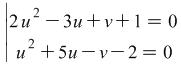Hint We replace $tema5_EN_files\tema5_EN_MathML_128.jpg$ and $tema5_EN_files\tema5_EN_MathML_129.jpg$ and the system is reduced to the following system $tema5_EN_files\tema5_EN_MathML_130.jpg$ . If you add together the equations of the new system you will get a quadratic equation $tema5_EN_files\tema5_EN_MathML_131.jpg$ .

Exercise 3.2. Solve the system 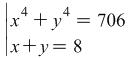$tema5_EN_files\tema5_EN_MathML_132.jpg$ .

Hint Again replace $tema5_EN_files\tema5_EN_MathML_133.jpg$ and $tema5_EN_files\tema5_EN_MathML_134.jpg$ and keep in mind that $tema5_EN_files\tema5_EN_MathML_135.jpg$ .